[数学・論理学の限界？]自己言及のパラドックスとは？４つの例と証明

対象読者

• 高校数学の「論理と集合」が分かる方

結論

自己言及とは、「この主張は○○だ」のように自身を含む主張のことだ。このような主張はおかしな結論を導く。これが自己言及のパラドックスだ。

以下では、自己言及のパラドックスの一般論とその具体例

1. 人食いワニのジレンマ
2. 攻殻機動隊の思考戦車「タチコマ」の発言
3. 嘘つきのパラドックス
4. ラッセルのパラドックス

について説明する。

その後に、実は自己言及のパラドックスとは矛盾というよりは、自然言語で表された命題を扱いきれない数学・論理学の限界を示していることを述べる。

自己言及のパラドックスの一般的構造

まずは自己言及のパラドックスの一般的構造を示す。

自己言及する命題を\(S\)と置く。

否定の自己言及

「\(\lnot S\)という主張」を\(S\)とおいた場合を考えてみる。

\(S\)を真だと仮定する。すると、\(\lnot S\)が成り立つことを意味し、仮定と矛盾する。

逆に\(S\)を偽だと仮定すると、\(\lnot \lnot S \equiv S\)となり、仮定\(\lnot S\)と矛盾する。

以上から、\(S\)を真と偽どちらと仮定してもパラドックス(矛盾)を引き起こす。

肯定の自己言及

次は、「\(S\)という主張」を\(S\)とおいた場合を考えてみる。

\(S\)が真だと仮定する。すると、\(S\)が成り立つことを意味するが、何の問題もない。

逆に\(S\)が偽だと仮定する。つまり、\(\lnot S\)が成り立つが、これも仮定と矛盾しない。

以上から、\(S\)は真と偽どちらでもOKというおかしなことになる。

以上が自己言及のパラドックスの一般だが、なんだか言葉遊びみたいで面白くない。なので、以下で自己言及のパラドックスの具体例を４つ挙げる。その後にこのパラドックスの正体を明かす。

人食いワニのジレンマ(ワニのパラドックス)(参考※１)

ワニが子供を襲った。

グへへ、美味そうなガキだぜ

私の子供を食べないで！

今日、ワシが何をするか当てられたら、子供は食わずに返してやろう

だが、ハズレたら食う！

さて、お母さんは何と答えるべきだろうか。どういう巡り合わせか、お母さんはつい先ほど、自己言及のパラドックスについての記事を読んでいた。

クソ！

なんでこんな時に自己言及のパラドックスのことが頭を離れないの？

……ハッ！！

その時・・・・！　圧倒的　閃きっ・・・・・・・・・・！！

あ、あなたはその子を食べる…!!

ワニが子供を食べる場合、母親はワニの行動を言い当てたことになるので、ワニは約束を破ったことになってしまう。

逆に食べなかった場合、母親の予想はハズレたことになり、子供を食べなければならなくなって、矛盾する。

ワニの行動によってワニの行動が決まる、という自己言及的な約束が仇となった。

人食いワニのジレンマ(ジョジョパロディ)[引用 参考※5]

攻殻機動隊の思考戦車「タチコマ」の発言(参考※4「原文ママ」)

タチコマ「僕は嘘しかつかない。本当のことは何一ついわないんだ。」

さて、もし今のセリフが本当なら、彼は今、真実を語ってしまった。
もし今のセリフも嘘なら、彼は普段から真実を語ることになる。この矛盾をどう処理する？

このタチコマの問題は嘘つきのパラドックス(クレタ人のパラドックスとも)と言われている。

嘘つきのパラドックス

嘘つきのパラドックスとは、「私は嘘つきである」と言う人が嘘つきなのかどうかは論理的に判定できないことを指す。

このような発言をした人をAさんとする。

Aさんが正直者である場合、この発言は矛盾している。だって、正直者ならば、「私は嘘つきだ」なんて嘘は言わないから。

Aさんが嘘つきである場合も、この発言は矛盾している。だって、嘘つきなのに「私は嘘つきだ」と正直に答えているから。

いずれにせよ、Aさんは正直者かつ嘘つきである、というおかしな結論を得る。これは上記の一般論「否定の自己言及」と同じだ。

逆に、Aさんは「私は正直者だ」と言ったとしても、「肯定の自己言及」と同様に正直者でも嘘つきでもOKとなり、何かがおかしい。

ラッセルのパラドックス

ラッセルのパラドックスとは、「自分自身に属さない集合」という自己言及的な集合を考えると矛盾が生じることを指す。これは集合論という数学の根底を揺るがす大問題だ(※補足)。

唐突になんだ？「集合が自分自身に属するかどうか」、なんて言われてもピンと来ないと思う。なので、次の「人々は人なのか」議論を見て欲しい。

一定の目的のもとに集まった人々のことを法人といい、法律上では一人の人間として扱う。特に、営利目的の法人のことを会社という。国という人の集合も擬人化されたりして、一人の人間と見做すことがある。

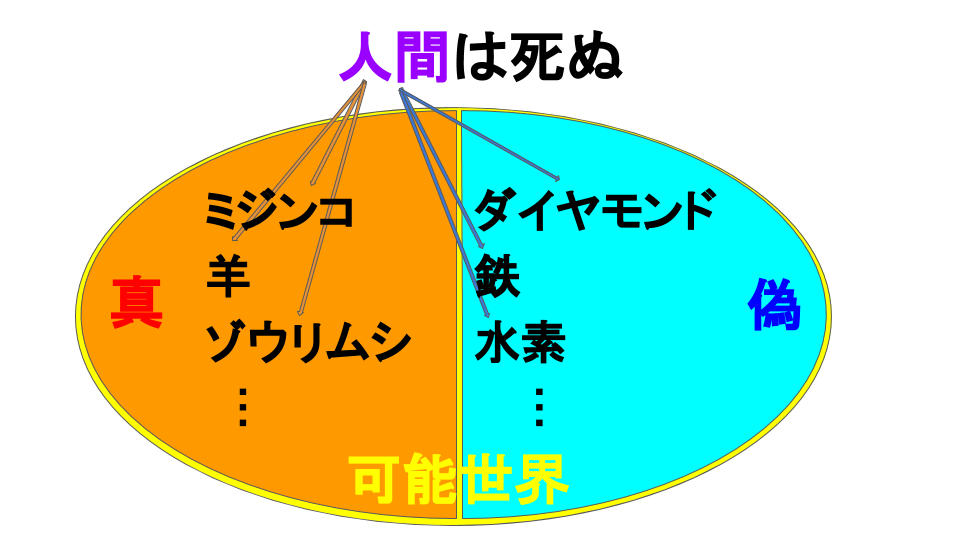
全人類を集めたものを\(S\)とおいてみる。全人類も法人や国のようにヒトなのだろうか。だとすると、\(S\)は人全てが属するはずなので、\(S \in S\)となる。いやいや、人とは個人に限ると考えると、\(S \notin S\)となる。

このように、「自分自身に属さない集合」は突飛な考えではない。前置きが長くなったが、矛盾を示そう。

自分自身に属さない集合を全て集めた集合を\(X\)とおく。

$$ X = \{S | S \notin S\} $$

\(X\)は自分自身に属す、つまり\( X \in X\)と仮定すると、\(X\)の要素は自分自身に属さない(\(X \notin X\))という定義と矛盾する。

逆に\(X \notin X\)と仮定すると、\(X\)は「自分自身が属さないものを全て集めた」集合なので、\(X \in X\)となり矛盾する。

命題関数を命題と言い張ることがパラドックスの原因(参考※２)

実は自己言及のパラドックスの根拠は背理法である。背理法は、その命題自体を証明するのではなく、「仮定は正しくない」ことを証明するに過ぎない。仮定\(S\)と結論\(\lnot S\)が排中律(真でも偽でもない、ということはない)に違反している。だから、途中の推論が正しかったとすると、仮定が間違っていた。これが背理法だ。

ならば、この矛盾を解くカギは普通の背理法のように、「仮定は偽である」とするのではなく、「仮定の設定自体が間違っていた」、つまり「仮定はそもそも命題ではなかった」と捉えることである。

「かつ」や「または」のように、命題の入力に対して真理値を返す関数を論理演算子と呼ぶ。一般に、真理値を出力する関数を命題関数という。命題関数は入力が確定しない限り真理値が確定しない。つまり命題関数は命題ではない。

自己否定している文「”この命題”は正しくない」は命題ではなく、論理演算子だったのではないか。入力した命題\(S\)の真理値を反転させるような論理演算子「\(S\)は正しくない」を否定演算子という。通常は\(“\lnot” S\)のように書くが、これを\(f\)とおく。”この命題”は\(f\)に対応するので、自己否定している文は\(f(f)\)と書き直せる。論理演算子の入力は命題でなければならないのに、関数を入力してしまっている。命題関数(論理演算子)を命題と言い張り、不適切な入力を行ってしまったことが自己言及のパラドックスを引き起こしたのだ。

数学・論理学の限界

なぜこんな間違いをおかしてしまったのだろうか。それは、意味が曖昧な自然言語による文を数学的に扱うためには、無理やりにでもその文を命題として解釈しなければならないからだ。

言語との向き合い方としては次のような３つの立場がある。

1. 構文論：　語句と語句の関係(文法)
2. 意味論：　語句とその内容の関係(意味)
3. 語用論：　語句と話者の関係

数学や論理学は、意味論の範疇にある。意味に着目しているからこそ、その文が正しいか、間違っているかを解釈できる。つまり、その文を命題として扱えるのだ。

文を解釈する(意味論に落とし込む)作業を行うのは読者であり、これは語用論の範疇に含まれる。大体の場合は文の解釈でおかしなことは起こらないが、自己言及的な文のように難解な場合は、語用論がネックとなってしまう。このように、数学には、真とも偽とも判定できないような問題が存在する。

補足

集合とは「区別できる要素を集めたもの」である、という素朴な定義ではラッセルのパラドックスが生じてしまう。この矛盾を回避するために集合に取り決めを導入した。これを公理的集合論という。どうやら数学は危機を免れたようだ。

参考

1. 詭弁論理学[野崎 明弘]
2. 論理学入門 [三浦 俊彦]
3. 法学入門[遠藤 浩, 久保田 きぬ子]
4. 【問題】自己言及のパラドックス【攻殻機動隊】
5. 考えるのをやめたキャラたち