対象読者
- 数学の問題を解く上で、必要条件・十分条件を見分けることはできるが、理解はできない方
- 会話で必要条件、十分条件を使いこなし、ちょいインテリ感を演出したい方
結論
必要条件と十分条件ってどっちがどっちだかややこしい。この判別が数学のセンター試験で出てくる。解き方を暗記して突破したものの、どんな意味なのか分からない方は多いのではないだろうか。
おさらいすると、
- 命題(条件)同士の力関係において、強い方を十分条件、弱い方を必要条件、
- 命題を満たす集合同士の包含関係において、小さい方を十分条件、大きい方を必要条件
という。何をもって強弱?、どんな観点から必要とか十分と言ってるのか。本記事では、なぜ、必要条件と十分条件と名付けられたのかを数学の定義から遡って解説することで、
- 丸暗記ではなく、
- 数学の問題も解けるし、
- 日常会話でも使いこなせる
ような理解を提供する。
また、その理解のチェックとして、最後に数学と日常会話の例題をおいた。
必要条件、十分条件は2つの条件の関係を表す用語
2つの条件を\(P\)と\(Q\)と書くことにする。例えば、
- Pを、「ぼくの好きな食べ物はリンゴです」
- Qを、「地球は青かった」
みたいにマジで適当な条件を選んだとする。このとき、\(P\)と\(Q\)には何の関係もない。何が言いたいかというと、必要条件と十分条件という言葉は、特定の関係を持つ2つの条件に対して使うものだということだ。
その関係とは、ずばり、「\(P\)ならば\(Q\)」が成り立つ(真となる)ような関係だ。これを掘り下げるためには、「ならば」は数学ではどう扱われるかを理解しなければならない。
数学の「ならば」の定義
数学における「ならば\(\Rightarrow\)」は、2つの真理値\(P\)、\(Q\)の入力に対して、1つの真理値を出力する2項演算子だ。足し算が2つの数値を受け取って、1つの数値を返すのと同じ感じだ。
\(P\)と\(Q\)を「命題」とする。命題とは、真か偽かのいずれかとして判断できる文のことだ。
\(\{1,2,\dots\}\)を自然数というのと同じで、\(\{真、偽\}\)を「真理値」という。
真理値は2通りある。よって、\(P\)と\(Q\)の演算の結果は2×2=4通りある。以下に「\(\Rightarrow\)」の入出力の対応表をまとめる(真理値表という)。
| \(P\) | \(Q\) | \(P \Rightarrow Q\) | |
| ① | 真 | 真 | 真 |
| ② | 真 | 偽 | 偽 |
| ③ | 偽 | 真 | 真 |
| ④ | 偽 | 偽 | 真 |
これが数学における「ならば」の定義だ。
いきなり表で「ならば」を定義されても意味が分からない、という方はこちらをどうぞ。
必要条件と十分条件の命名理由
必要条件、十分条件を考える上で、表1.②となるような状況は無視する。その主張\(P \Rightarrow Q\)が成り立たないようなデタラメな状況には興味ないからだ。
状況を表1の①、③、④に限定することで、一方の真偽がもう一方の真偽を制約するような、条件間の力関係が見えてくる。
いきなりだが、以下のようなゲームがあるとする。
- \(P\)と\(Q\)の真偽は不明である
- 片方は真である
- もう片方の真理値を推定せよ
このとき、\(P\)と\(Q\)のどちらが真だと嬉しいだろうか。場合分けして考える。
- \(P\)が真の時、\(Q\)も真であることが確定する(表1.①)
- 逆に、\(Q\)が真の時、\(P\)は真にも偽にもなり得る(表1.①③)
これは、「\(P\)が\(Q\)の真理値を強制している」、ということを示している。以下のようにも言い換えられる。
- \(P\)は\(Q\)よりも強い。
- 逆に言えば、\(Q\)は\(P\)よりも弱い。
さらに別の言い方もできて、
- \(P\)が真であることさえ分かれば、\(Q\)の真理値を知るのに十分だ
- 逆に\(P\)が真であるためには、少なくとも\(Q\)は真である必要がある
故に、\(P\)は\(Q\)の十分条件、\(Q\)は\(P\)の必要条件という。
実は、十分条件と必要条件には別名があって、
- 十分条件\(P\)を強い命題
- 必要条件\(Q\)を弱い命題
という。もはや説明は要らないだろう。
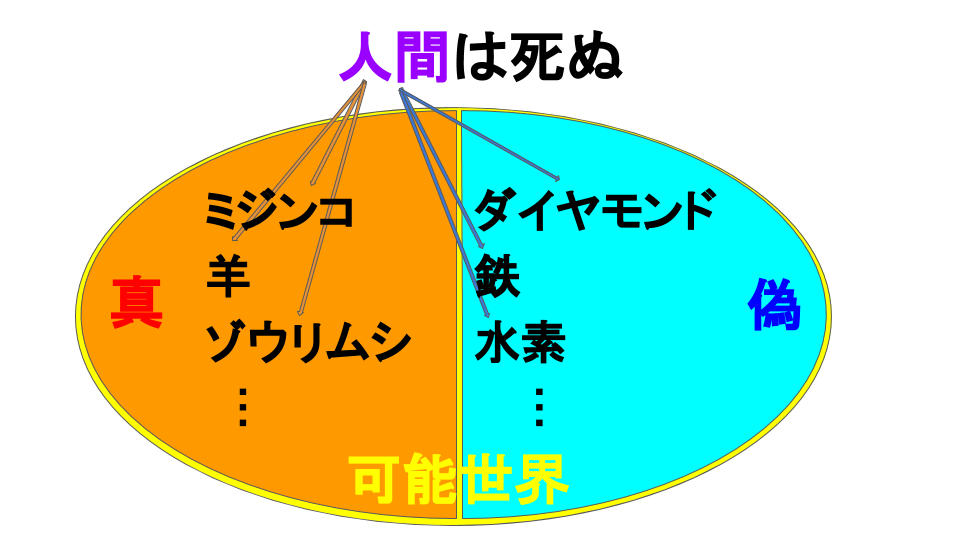
十分条件は必要条件に含まれる
以上は、表からの説明だった。さらに図解があれば理解の助けになる。そこで、十分条件や必要条件には包含関係が成り立つことを確認する。
実は命題は、主語と述語に分解できる。
- 主語は区別できる要素
- 述語は性質
を表す。例えば、「俺様はモテモテだ」という命題は、全世界のモテ男の集合を\(S\)とおくと、\(s \in S\)と書ける。「これにはこういう性質がある」ということを数学では集合を用いて表すことができる。
以下のような命題を考える。
- \(P\)は\(Q\)の十分条件である
- \(P\)と\(Q\)は同じ主語を持つ
命題\(P\)を満たすもの全ての集合を\(P’\)、命題\(Q\)のそれを\(Q’\)とおく。このとき、以下のように書ける。
$$ s \in P’ \Rightarrow s \in Q’ $$
十分条件では表1.②のような状況は考えないので、この式は常に真となる。
あれ?。これは、集合の包含関係じゃないか。そう、十分条件\(P\)は必要条件\(Q\)に含まれるのだ。
条件が強いほど、小さな集合となる
条件の強さとは、条件の制約の厳しさを意味する。
例えば、以下の条件は番号が若いほど、制約が多く、強い(厳しい)条件だ。
- Aさんは日本人である
- Aさんはアジア人である
- Aさんは地球人である
若い番号の条件が十分条件、それより大きい番号の条件は必要条件に対応する。

図1.条件の包含関係
十分条件が満たされれば、必要条件も自動的に満たされる。言い換えれば、十分条件は同時に必要条件をも満たす。これは上で見た包含関係からも明らかだ。十分条件の方が必要条件よりも超えるべきハードルがたくさんあり、十分条件を満たす集合は必要条件のものよりも小さくなる。
最強の条件と最弱の条件
では、最強の条件、最弱の条件とはどんなものだろうか。まずは命題の観点から、次は集合の観点から考えてみる。
最強の命題には、制約が厳しすぎて、もはや、条件を満たす(真となる)ものが存在しないのだ。逆に、最弱の命題は制約が緩すぎて、なんでもOK、すべて正解(真)としてしまう。つまり、
- 最強の命題とは、常に偽となる命題であり、
- 最弱の命題とは、常に真となる命題のことだ。
次は集合の観点だ。条件が強くるほど、それを満たす集合も小さくなったのだから、
- 最強の条件とは、大きさゼロの集合、つまり要素を何も持たない空集合であり、
- 最弱の集合とは、議論対象をすべて含んだ集合(普遍集合という)だ。
数学や日常会話で必要条件・十分条件を使いこなす
以上で、必要条件・十分条件とは、2つの命題の力関係、包含関係を示す用語であることを確認した。
包含関係という視点は、数学の問題を解くのに使える。力関係という視点は、日常会話において、必要条件・十分条件というワードを使いこなす助けとなる。
以下では、例題を通して、このことを確認する。
数学の「論理と集合」の問題
適当な数学の問題を参考※2よりいくつか引用する(※筆者注)。
以下において、\(P\)は\(Q\)の何条件であるか、それぞれ答えよ。ただし、xは実数とする。
- \(P: x = 3, Q: x^2 – 4x + 3 = 0\)
- \(P: x > 0, Q: |x| > 1\)
\(P\)を満たす集合を\(P’\)、\(Q\)を満たす集合を\(Q’\)とおく。
問1は、\(P’ = \{3\}, Q’ = \{1, 3\}\)であり、\(P’ \subset Q’ \)。よって、十分条件。
問2は、 \(P’\)と\(Q’\)の間には包含関係が成り立たない。よって、十分条件でも必要条件でもない。
この程度の問題を解くためだけなら、他のサイトなどであるように、語呂合わせとかのテクニックで暗記すれば十分だ。しかし、それだけの理解では、日常会話には通用しない。
日常会話での必要条件・十分条件
とある発言シーンを雑考する。

俺様が天才であることは、この問題が解けることの十分条件だ!
この男は何を言ってるのだろうか。俺様の天才具合をアピールしたいのだろうか。それとも、天才の力を以ってしても、その問題は難しい、と言いたいのだろうか。
まずは、「十分条件」と言ってる以上、「天才」という性質と、「この問題が解ける(能力を有する)」という性質は無関係なものではなく、力関係が成り立つことを主張している。そして、「天才」の方がより強力な条件であり、天才ならば当然その問題は解ける、と言ってる。
この男が自身満々にそう発言している場合、
- 「自分は天才であることは真だ」と確信しており、
- 当然、俺はその問題を解ける
と尊大な態度を取っていることが分かる。
逆に自信なくそう言っているのだとしたら、
- 「この問題」とは天才にとっては簡単なことは周知の事実であり、
- それにも関わらず、もし自分が解けなかったら…
とプレッシャーを感じている、と読むことができる。
以上のように、。必要条件・十分条件の意味が分かっていれば、その発言に込められた気持ちがより分かるかもしれないし、自分の強い気持ちを伝えることもできるかもしれない。そもそも、必要条件・十分条件なんて、日常でそんなに聞かないけどw。
参考
- 論理学入門 [三浦 俊彦]
- スタディサプリ[必要十分条件]


コメント